Water Surface Increase Calculation for Wall Openings

I present here the method used by NPS Global Engineers for calculating the post-development water surface increase due to a wall with standardized openings. This method has been accepted for multiple projects (including APN 211-44-273, 216-67-067B, 216-67-067A, 219-40-293J, 211-45-084B, 211-47-031, 211-51-031G, 211-51-020K, 211-51-031K, and 503-51-966M) by Maricopa County Planning and Development.

Introduction

Site walls often span varying flow conditions, especially in areas of alluvial flow where we may have a 2D model of pre-development flow conditions. We organize our analysis of such a wall by dividing it into segments analogous and similar (though not necessarily exactly corresponding) to standard CMU "Dooley" (alternately "dually") wall panels. We assign a unique ID to each panel (or hydraulically similar reach), and we analyze each panel (or reach) using a spreadsheet that has two tables. Table 1 calculates standard flow obstruction factors for various types of wall opening. Table 2 uses the standard factors from Table 1 to calculate the water surface elevation increase for each wall section (panel or reach) ID.

Wall openings analysis spreadsheet example Table 1

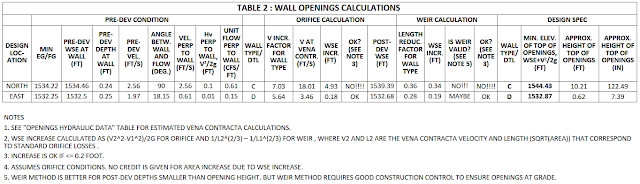Wall openings analysis spreadsheet example Table 2

Design Considerations

Bottom of openings

To approximately provide the required open area as analyzed, the bottom of wall openings must be at or below the pre-development grade. While this is impossible to accomplish perfectly on sloping terrain and difficult to accomplish consistently under any condition, construction specifications must state the requirement.

Top of openings

To approximately provide the required open area as analyzed, the top of wall openings must be at or above the post-development water surface elevation. For turned blocks or missing blocks, there must be enough rows to cover the entire flow depth. For lintels, the bottom of the lintel (top of the opening) must be at or above the post-development water surface elevation.

Analysis Considerations

Vena Contracta

Flow going through an orifice or entering a pipe experiences contraction of the jet unless there is carefully adequate rounding of the entrance. Since rounding of turned block openings is not feasible, we include a "Reference orifice coefficient, Cd" in Table 1. To simplify analysis, we conceptualize this as being entirely an contraction coefficient, Cc, even though it is a combination of a contraction coefficient, Cc (typically 0.61 for a sharp-edged orifice), and a velocity coefficient, Cv (typically 0.98 for a sharp-edged orifice).

Post-development Reduced Flow Area

We calculate area and dimension reductions and corresponding factors in Table 1 based on our hypothetical vena contracta area compared to the assumed pre-development area. We use these reductions in our calculations in Table 2.

We assume the pre-development area based on the hypothetical panel length and row height. See total panel length and total assumed height in Table 1.

We calculate the post-development cross-sectional flow area based on the opening size, vena contracta, and clogging. Since we use these methods also for lintel openings (beams and piers), we also estimate the vena contracta jet separation so that we can account for separation only at the sides (piers) of a lintel opening assuming that lintels are always specified to be above the post-development water surface elevation.

Water Surface Elevation Increase Calculation

Since our 2D or 1D (including uniform flow calculation) models give us the useful pre-development parameters of velocity, depth, and flow direction, we start with those. 

Flow Direction

We use the flow direction to determine outside the spreadsheet the approximate angle between the wall and the flow direction where 90 degrees means wall and flow direction are perpendicular.

Velocity and Flow Perpendicular to the Wall

We calculate the pre-development velocity, velocity head, and unit flow perpendicular to the wall since these are the component that we must handle with openings.

We iteratively select a wall design on Table 2 referring to the types defined in Table 1. Based on that, we look up the velocity increase factor.

Velocity at Vena Contracta

The post-development velocity at the vena contracta is simply the pre-development velocity times the velocity increase factor.

Clogging

We include a clogging factor that reduces our effective area as a factor of safety depending on the conditions or the review requirements.

Orifice Method

Applicability

The orifice method applies assuming that depth is greater than the top of the wall openings.  This method conservatively ignores the transition range between weir flow and orifice flow. Also, the depth assumption is always a conservatively invalid assumption since we are specifying that the top of the wall opening must be at or above the post-development water surface elevation and therefore the post-development cross-sectional flow area is variable like a weir instead of fixed like an orifice. This misapplication may be unacceptably conservative for depths that are very small compared to a single row of openings.

Water Surface Increase

We equate water surface increase to velocity head increase at the vena contracta. This is based on a stated assumption that 100% of the velocity head increase at the vena contracta is lost. This corresponds roughly to the standard assumption of a pipe exit loss coefficient of 1.

Velocity Increase Factor

We calculate velocity head increase (loss) using a velocity increase factor from Table 1. This velocity increase is inversely proportional to the area reduction in Table 1.

WSE Increase

The water surface elevation increase is the difference in the velocity heads between post-development and pre-development:

deltaH = Vpost^2 / (2*g) - Vpre^2 / (2*g)

= (Vpost^2 - Vpre^2) / (2*g)

Weir Method

Applicability

The weir method applies in the ideal case where pre-development depth is lower than the top of the wall openings. This assumption only applies strictly for lintels or where the depth is lower than the top of a single row of openings. This assumption and the method are also invalidated to some extent by the non-feasibility of specifying the exact elevation of every reach of a wall. Since wall openings fall wherever they may fall, we can't really guarantee that the bottom of openings is at or below grade except at a lintel. But the weir method may be a good check on the gross invalidity of the orifice method where depths are very small.

Length Reduction Factor

We calculate water surface elevation increase using a weir length reduction factor from Table 1 that is based on our hypothetical vena contracta jet separation on Table 1

Water Surface Increase

We calculate the weir water surface increase as follows:

Q = Cw * L * H^1.5; Weir equation

H = [Q / (Cw * L)]^(2/3)

deltaH = H2 - H2 = [Q / (Cw * L2)]^(2/3) - [Q / (Cw * L1)]^(2/3)

=  [Q / (Cw * L2)]^(2/3) - [Q / (Cw * L1)]^(2/3)

Since L2 = L1 * Fl,

deltaH = H2 - H2 = [Q / (Cw * L1 * Fl)]^(2/3) - [Q / (Cw * L1)]^(2/3)

= (Q / Cw)^(2/3) * [1/(Fl * L1)^(2/3) - 1/L1^(2/3)]

= (Q / Cw)^(2/3) * [1/Fl^(2/3) * 1/L1^(2/3) - 1 * 1/L1^(2/3)]

= (Q / Cw)^(2/3) * [1/Fl^(2/3) - 1] / L1^(2/3)

And since for unit flow, L1 = 1,

deltaH = (q / Cw)^(2/3) * [1/Fl^(2/3) - 1] / 1^(2/3)

 = (q / Cw)^(2/3) * [1/Fl^(2/3) - 1]; Weir Calculation WSE increase in Table 2